quadrilateres

Figures élémentaires de géométrie : les quadrilatères

I- Généralités

Définition :

On appelle quadrilatère toute figure composée de 4 sommets et 4 côtés (chaque sommet est le point de départ de deux segments).

Exemple :

Etude de quelques quadrilatères (convexes) particuliers

1- Le trapèze

Définition :

On dit qu’un quadrilatère (convexe) est un trapèze lorsque 2 de ses côtés sont parallèles.

Exemple :

Définition :

On appelle trapèze rectangle un trapèze ayant un angle droit.

Exemple :

Définition :

On appelle trapèze régulier un trapèze dont les côtés obliques ont la même longueur.

Exemple :

2- Le parallélogramme

Définition :

On dit qu’un quadrilatère est un parallélogramme lorsque ses côtés opposés sont parallèles 2 à 2.

Exemple :

Propriété 1 :

Un parallélogramme admet un centre de symétrie qui est le point d’intersection de ses deux diagonales.

Exemple :

Conséquences : a) Les diagonales d’un parallélogramme se coupent en leur milieu.

b) Les angles opposés d’un parallélogramme ont la même mesure.

c) Les côtés opposés d’un parallélogramme ont la même longueur.

Remarque : un parallélogramme est un trapèze particulier.

Propriété 2 :

Un quadrilatère (convexe) ayant 2 côtés parallèles et de même longueur est un parallélogramme.

Propriété 3 :

Un quadrilatère (convexe) ayant les côtés opposés de même longueur est un parallélogramme.

II- Etudes de parallélogrammes particuliers

1°- Le rectangle

Définition :

Un rectangle est un quadrilatère ayant 4 angles droits.

Exemple :

Remarque : un quadrilatère ayant 3 angles droit a forcément 4 angles droits.

Propriétés :

a) Un rectangle est un parallélogramme qui a un angle droit.

Ou bien, autre façon de voir :

b) Un rectangle est un parallélogramme dont les diagonales ont même longueur.

Exemple :

Réciproquement :

a) Un parallélogramme ayant un angle droit est un rectangle.

b) Un parallélogramme dont les diagonales ont même longueur est un rectangle.

2°- Le losange

Définition :

Un losange est un quadrilatère dont les 4 côtés sont de même longueur.

Exemple :

Propriétés :

a) Un losange est un parallélogramme qui a 2 côtés consécutifs de même longueur.

Ou bien, autre façon de voir :

b) Un losange est un parallélogramme dont les diagonales sont perpendiculaires.

Exemple :

Réciproquement :

a) Un parallélogramme ayant 2 côtés consécutifs de même longueur est un losange.

b) Un parallélogramme dont les diagonales sont perpendiculaires est un losange.

3°- Le carré

Définition :

Un carré est un quadrilatère à la fois rectangle et losange.

Exemple :

Un carré possède donc à la fois toutes les propriétés des rectangles et des losanges.

Sachant qu’un quadrilatère est un carré, on peut dire :

les 4 angles sont droits

les côtés opposés sont parallèles

les 4 côtés ont même longueur

les côtés consécutifs sont perpendiculaires

les diagonales se coupent en leur milieu, ont même longueur et sont perpendiculaires.

Exemple :

III- Récapitulatifs des propriétés des quadrilatères

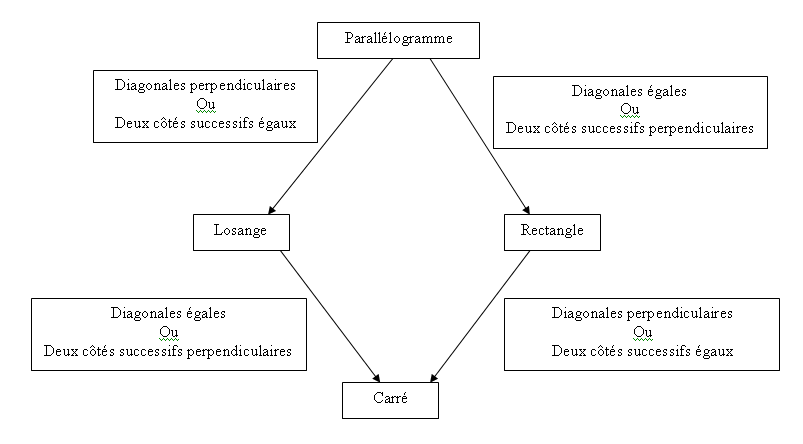
En suivant le sens des flèches :

on obtient le quadrilatère suivant en ajoutant une des propriétés encadrées aux propriétés du quadrilatère précédent.

tout quadrilatère a toutes les propriétés des quadrilatères qui le précèdent.

Tableau des propriétés des quadrilatères :

Propriétés	Parallélogramme	Rectangle	Losange	Carré
Des côtés
Côtés opposés parallèles	Oui	Oui	Oui	Oui
Côtés opposés égaux	Oui	Oui	Oui	Oui
Côtés successifs égaux	Non	Non	Oui	Oui
Côtés successifs perpendiculaires	Non	Oui	Non	Oui
Des angles
Angles opposés égaux	Oui	Oui	Oui	Oui
Angles successifs supplémentaires	Oui	Oui	Oui	Oui
4 angles droits	Non	Oui	Non	Oui
Des diagonales
Diagonales qui se coupent en leur milieu	Oui	Oui	Oui	Oui
Diagonales égales	Non	Oui	Non	Oui
Diagonales perpendicualires	Non	Non	Oui	Oui
Des axes et centre de symétrie
Un centre de symétrie	Oui	Oui	Oui	Oui
Nombre d'axes de symétrie	0	2	2	4