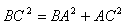
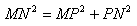
Le théorème de Pythagore

Retour  index chapitres


Dans un triangle rectangle, on appelle hypoténuse le coté qui fait face à l’angle droit.

Remarque : dans un triangle rectangle, l’hypoténuse est toujours le côté le plus long.


I- Le théorème de Pythagore

1- Le théorème

Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux côtés de l'angle droit.



Exemple 1

Si on sait que ABC est un triangle rectangle en A, alors on peut écrire :

Exemple 2

Si on sait que MNP est un triangle rectangle en P, alors on peut écrire :


2- Utilisations

Lorsque l’on sait qu’un triangle est rectangle et que l’on connaît la longueur de deux côtés de ce triangle, alors ce théorème permet de calculer la longueur du troisième côté.

Ce théorème permet aussi de démontrer qu'un triangle n'est pas un rectangle (voir exercice 4).

3- Exercices résolus

Exercice 1

On considère un triangle PQR, rectangle en P, tel que PQ = 6 cm et PR = 8 cm.

Calculer la longueur QR.



Solution :

Appliquons le théorème de Pythagore dans le triangle PQR rectangle en P. On obtient :


Donc :


Exercice 2

On considère un triangle DEF, rectangle en E.

Calculer la longueur DE sachant que DF = 12 cm et EF = 7cm.



Solution :

Appliquons le théorème de Pythagore dans le triangle DEF rectangle en E. On obtient :


Donc :



II- La réciproque du théorème de Pythagore

1- La réciproque

Si on sait que dans un triangle la somme des carrés de deux côtés est égale au carré du troisième côté, alors ce triangle est un triangle rectangle.



Exemple :

On sait que :


On peut donc conclure que l’angle est un angle droit

( c'est-à-dire ABC est un triangle rectangle en A ).

2- Utilisation

Lorsque l’on connaît la longueur des côtés d’un triangle mais que l’on ne connaît pas la nature du triangle, pour savoir s’il est rectangle, on regarde si l’égalité de la réciproque de Pythagore est vérifiée.

On reconnaît ainsi si un triangle est rectangle ou non.

3- Exercices résolus

Exercice 3

Le triangle EFG tel que EF = 3 cm, EG = 4 cm et FG = 5 cm est-il un triangle rectangle ?

Solution :

Pour savoir si le triangle EFG est rectangle, on calcule le carré de la longueur du plus grand côté (lui seul peut éventuellement être l'hypoténuse) :


On calcule ensuite, séparément, la somme des carrés des longueurs des deux autres côtés :

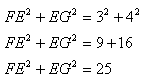
On a donc :

Ici, les deux résultats sont égaux donc, d'après la réciproque du théorème de Pythagore, le triangle EFG est rectangle en E.

Exercice 4

Le triangle ABC, tel que AB = 3 cm, AC = 5 cm, BC = 6 cm est-il un triangle rectangle ?

Solution :

Pour savoir si le triangle ABC est rectangle, on calcule le carré de la longueur du plus grand côté (lui seul peut éventuellement être l'hypoténuse) :


On calcule ensuite, séparément, la somme des carrés des longueurs des deux autres côtés :

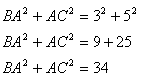
On a donc :

Ici, les deux résultats obtenus sont différents donc, d'après le théorème de Pythagore, le triangle ABC n'est pas un triangle rectangle (ni en A, ni en B, ni en C !)

Remarques très importantes :


Dans ce cas de figure (exercice 4), d'un point de vue logique, ce n'est pas la réciproque du théorème de Pythagore qui permet de conclure, mais le théorème lui-même !


Il est inutile (exercice 4) de vérifier les autres égalités possibles : si celle essayée ci-dessus n'est pas vérifiée, les autres ne le seront pas non plus !