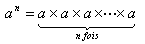
PUISSANCES
I- Définitions
1- Puissances positives d’un nombre
Soit a un nombre non nul et n un entier naturel ( positif ).
|
|
|
|---|
|
|
se dit « a puissance n » ou « a exposant n » |
|---|
n s’appelle l’exposant ou la puissance.
Cas particuliers
|
Carré d’un nombre a : |
|
« a puissance 2 » se dit aussi « a au carré ». |
|---|---|---|
|
|
|
|
|
Cube d’un nombre a : |
|
« a puissance 3 » se dit aussi « a au cube ». |
Conventions
|
|
|
|
|---|
|
Exemples : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Remarque : considérons un nombre a négatif.
Cas d’une fraction
|
|
|
Démonstration
|
Exemple : |
|
2- Puissances négatives d’un nombre
Soit a un nombre non nul et n un entier naturel ( positif ).
Convention
|
|
|
Par convention, |
|
désigne l’inverse du nombre a ! |
|---|
|
Exemples : |
|
|
|
|
 |
|
|
|
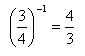Cas général :
|
|
|
|---|
|
|
est l’inverse de |
|
|---|
|
Exemples : |
|
|
|
|
|
|
|
|
|
Cas particuliers
|
Puissances de 10 |
|
ou n chiffres après la virgule |
|---|
|
Exemples : |
|
|
|
II- Propriétés des puissances
Soit a et b deux nombres non nuls et n et m deux entiers relatifs.
Formule 1
|
|
|
|---|
Démonstration
|
Exemples : |
|
|
|
|
|
|
|
|
|
Formule 2
|
|
|
|---|
Démonstration
|
Exemples : |
|
|
|
|
|
|
|
|
|
Formule 3
|
|
|
|---|
Démonstration
|
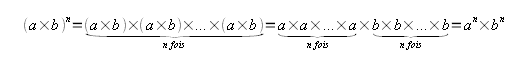
Exemples : |
|
|
|
Formule 4
|
|
|
|---|
Démonstration
|
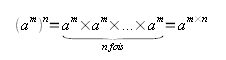
Exemples : |
|
|
|
|
|
|
On
dit qu’un nombre est en notation scientifique lorsqu’il
est écrit sous la forme «
» où a est
un nombre vérifiant 
(a peut être égal à
1 mais pas à 10) et n est un entier positif ou négatif.
Exemple :
Le
nombre 1 234,5 peut s’écrire :
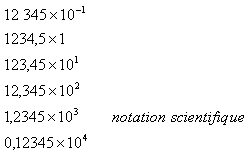
Tous les nombres peuvent s'écrire sous la forme scientifique !
Lorsqu'on utilise la notation scientifique d'un nombre, on arrondit très souvent le nombre à 2 chiffres après la virgule, ce qui donne un ordre de grandeur du nombre plus que suffisant dans la majeure partie des cas (« quand on parle d'une distance en kilomètres, on n'est pas à quelques mètres près finalement »).
Exemple : donner l'écriture scientifique de 29 367 543 135
