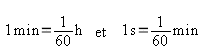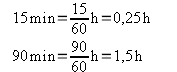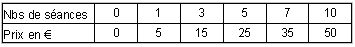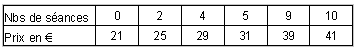Retour index chapitres
LA
PROPORTIONNALITE
I-
DEFINITION
|
Définition :
|
on dit
que deux séries de nombres sont proportionnelles lorsqu’on
passe d’une série à l’autre en
multipliant toujours par le même nombre.
Ce
nombre s’appelle le coefficient de proportionnalité.
|
Pour
représenter ces deux séries de nombres, on utilise très
souvent un tableau.
Exemples :
| a) |
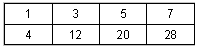 |
Coefficient de proportionnalité : 4 ou 0,25 |
| b) |
 |
Coefficient de proportionnalité : 5 ou 0,2 |
| c) |
Dans une station service, le prix à payer est proportionnel au
volume de carburant distribué.
Prix de l'essence : 1,34 € /L
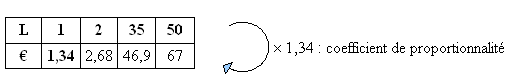
|
|
| d) |
Dans un supermarché, le prix des
fruits et légumes est proportionnel à leur masse.
Prix des patates : 0,95 € /kg
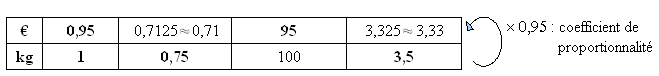
|
|
| e) |
Le carburant pour un motoculteur
est un mélange de super et d’huile où les doses d’huile et
d’essence sont proportionnelles : il faut 2 doses d’huile pour 3
doses de super.
Déterminer le coefficient de proportionnalité
qui permet d’obtenir la dose de super en fonction de la dose
d’huile.
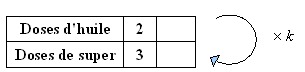
Le nombre k vérifie : donc 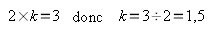
Le coefficient de
proportionnalité qui permet d'obtenir la dose de super en fonction
de la dose d'huile est 1,5.
|
|
II-
RECHERCHE D’UNE QUATRIEME PROPORTIONNELLE
Dans une situation de proportionnalité,
la quatrième proportionnelle est le quatrième nombre calculé à
partir de trois autres nombres déjà connus.
Pour calculer cette quatrième
proportionnelle, on peut utiliser l'une des cinq méthodes suivantes.
Selon les exercices, une méthode
sera plus simple que les autre. Il est donc nécessaire de
connaître toutes les méthodes.
Les calculs doivent apparaître
clairement lors de la rédaction de la réponse.
1- Coefficient de proportionnalité
On
recherche le coefficient de proportionnalité du tableau et
ensuite on le complète ( calculs sur les lignes ).
| Exemple : |
 |
coefficient de proportionnalité : 5 |
2- Retour à l'unité
On
recherche la valeur correspondant à la valeur 1 (« retour
à l'unité »)
Exemples :
| a) |
 |
|
| b) |
Dans
un supermarché, 21 kg de tomates coûtent 23,10 €.
Combien
coûtent 35 kg de ces tomates ?
21
kg coûtent 23,10 € donc 1 kg coûte 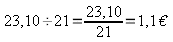
donc
35 kg coûtent 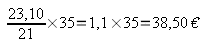
35 kg de ces tomates coûtent
38,50 €.
|
|
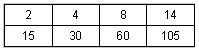
3- Additions ou soustractions de colonnes entre-elles
Règle : en additionnant (ou en soustrayant) deux colonnes entre-elles, on
obtient une nouvelle colonne du tableau.
Exemples :
| a) |
|
|
| b) |
 |
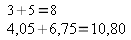 Les kg s'additionnent, donc les € s'additionnent ! Les kg s'additionnent, donc les € s'additionnent !
 |
4- Multiplication d'une colonne par un nombre
Règle : en multipliant (ou en divisant) par un même nombre une colonne,
on obtient une nouvelle colonne du tableau.
Exemples :
| a) |
La
prime annuelle d’un vendeur est proportionnelle au montant des
ventes qu’il a réalisées pendant l’année.
Le directeur du
magasin utilise le tableau suivant pour verser les primes à ses
vendeurs.
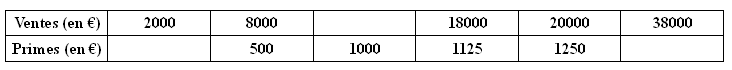
Les
ventes sont divisées par 4, donc la prime sont divisées par 4.
La
prime double par 2, donc les ventes doublent.
Les ventes
s'additionnent, donc
les primes s'additionnent.
|
Les
ventes sont divisées par 4, donc la prime sont divisées par 4.
La
prime double par 2, donc les ventes doublent.
Les ventes
s'additionnent, donc
les primes s'additionnent. |
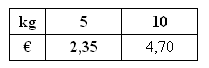
| b) |
Compléter le tableau suivant :
|
La quantité est multipliée par
2, donc le prix est multiplié par 2
|
Attention : on ne peut pas
multiplier entre-elles deux colonnes !
5- Produit en croix
| a) |
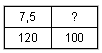 |
« On
multiplie la diagonale et on divise par le 3ième »
On
utilise la méthode du produit en croix.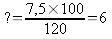
|
Remarque : une proportion
est une égalité de deux quotients. Dire que l’on a un tableau de
proportionnalité, c’est dire que l’on a l’égalité des
fractions formées par les lignes du tableau.
Exemple
Le tableau suivant
est un tableau de proportionnalité.
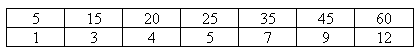
Ce tableau équivaut à dire que les
fractions 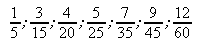 sont égales ou que les fractions
sont égales ou que les fractions 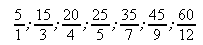 sont égales.
sont égales.
III-
QUELQUES SITUATIONS DE PROPORTIONNALITE
1- Pourcentages
Un pourcentage est une proportion
donnée par rapport à une quantité de 100 éléments : c'est donc
bien évidemment une situation de proportionnalité.
Exemple 1
Dans un collège, trois élèves sur
cinq possèdent un vélo.
Quel pourcentage des élèves du
collège possèdent un vélo ?
Solution
|
Cette situation revient à déterminer
le nombre x dans le tableau de proportionnalité suivant :

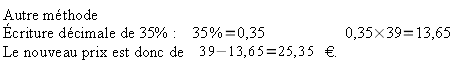 |
 Le nouveau prix est donc de : Le nouveau prix est donc de : 
|
Exemple 2
Une
enquête a révélée que sur 2000 personnes
interrogées, 80 avaient les yeux bleus.
1- En
supposant que la proportion des yeux bleus est la même dans
toute la population, quel est le pourcentage de personnes ayant les
yeux bleus ?
2- Dans un
village de 3500 habitants, combien de personnes auraient les yeux
bleus ?
Solution :
-
Sur
2000 personnes, 80 ont les yeux bleus. Cela se traduit par la
fraction
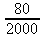 .
.
On veut transformer cette fraction en une fraction ayant pour
dénominateur 100.
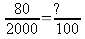
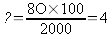
4 % des
personnes ont les yeux bleus, ce qui signifie que si on interroge 100
personnes, 4 vont avoir les yeux bleus
Remarque :
le calcul 80 ÷ 2000 donne
0,04 comme résultat .
0,04
signifie « 4 centième », c’est-à-dire
4 % !
2- 1ère
méthode :
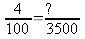
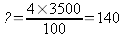
2ième
méthode : prendre 4% de quelque chose, c’est
multiplier ce quelque chose par 0,04
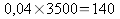
Sur 3500
personnes,140 personnes auront les yeux bleus.
Ce qu’il
faut retenir : prendre un pourcentage, c’est faire une
multiplication.
-
|
Prendre p % ,
c’est multiplier par
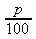
|
Remarque :
12 % est égal à 0,12
3 % est
égal à 0,03
5,1 %
est égal à 0,051
Augmentation
d’une somme
|
Si une quantité est
augmenté de a %, cela veut dire que cette quantité
est multipliée par
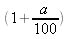
|
Exemple :
le prix d’une chemise a augmentée de 25 % . Avant
augmentation, la chemise coûtait 30 €.
Quel est
son nouveau prix ?
Le nouveau
prix est de :
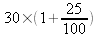
Remarque :
25 % = 0,25 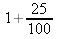 est donc égal à : 1,25
est donc égal à : 1,25
Le nouveau
prix de la chemise est de
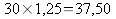 €
€
Diminution
d’une somme
|
Si une quantité est diminué
de a %, cela veut dire que cette quantité est multipliée
par
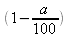
|
Exemple :
Le prix d’une chemise est diminué de 25 %. Avant
diminution, le prix était de 37,50 €.
Quel est
son nouveau prix ?
25 % =
0,25 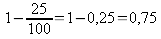
Le nouveau
prix de la chemise est de :
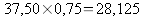
Remarque :
on ne retrouve pas le prix de 30 € !
2- Echelles
Lorsqu’on fait un plan, une carte,
on utilise une échelle.
Les dimensions sur le plan sont
alors proportionnelles aux dimensions dans la réalité.
L’échelle
du plan est le coefficient de proportionnalité
qui permet d’obtenir les dimensions sur le plan en fonction des
dimensions réelles.
Formule :
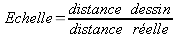
Attention
: pour utiliser cette formule, il est impératif
que toutes les dimensions
soient exprimées dans la même unité !
| Exemple |
Sur une maquette à l’échelle 1/48, quelle est la taille réelle
d’une pièce longue de 12 cm sur la maquette ?
Et la taille sur la maquette d’une pièce de 7,2 m de long dans la
réalité ?
|
|
Solution
|
L’échelle
1/48 s’interprète par : 1 cm sur le plan représente 48 cm dans la
réalité.
Cela
se traduit aussi par le tableau de proportionnalité suivant :

|
La
taille réelle d'une pièce longue de 12 cm sur la maquette est 576
cm (ou 5,76 m).
La taille sur la maquette d'une pièce de 7,2 m de
long dans la réalité est 15 cm.
|
3- Mouvement uniforme
a) Unités de temps
On peut exprimer une
durée à l’aide de nombres décimaux ou de fractions de durées :
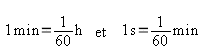
Exemple :
Exprime en heure
décimale les durées suivantes : 15 min et 90 min.
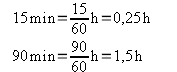
b) Vitesse
Lorsqu’on
se déplace à allure constante,
on parle de mouvement uniforme.
Dans
ce cas, la distance
parcourue est proportionnelle
à la durée.
Lorsqu’on
parle de la vitesse moyenne
d’un objet animé d’un mouvement uniforme, on considère que la
distance
parcourue est proportionnelle
au temps.
Remarque
: La vitesse est un coefficient de proportionnalité !
La
vitesse s'exprime par la formule :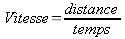
Attention
: pour utiliser cette formule, il est impératif
que le temps
soit exprimé en écriture décimale
!
Exemple :
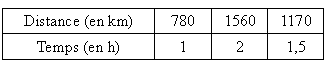
Un avion vole à
allure constante et a parcouru 780 km en une heure. Quelle distance
parcourra-t-il en 2 h ?
En 1 h 30 min ?
Solution
Puisque l’avion
vole à allure constante, le mouvement est uniforme. La distance
parcourue est donc proportionnelle à la durée du vol.
En
2 h, il couvrira ainsi une distance deux fois plus grande, égale à
:

c)
Conversions d’unités
Dans le système d'unité usuel
(international), les convertions d'unités sont des questions
de proportionnalité.
IV- Graphique
Le graphique d'une situationde proportionnalité est
forcément une droite qui passe par l'origine du repère,
c'est-à-dire par le point de coordonnées (0 ; 0).
Tout autre graphique ne peut pas correspondre à une situation de proportionnalité !
Exemple :
|
Un nouveau cinéma vient de s'installer dans une grande ville. Il propose deux tarifs à ses clients.
Tarif A : 5 € par séance
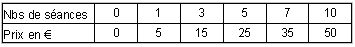
Tarif B : un abonnement de 21 € annuel et 2 € par séance.
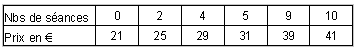
|
|
Le tarif A correspond à une situation de proportionnalité, ce qui n'est pas le cas du tarif B !
Remarque : pour 7 séances, les deux tarifs sont identiques
(point d'intersection des deux courbes), si on va à moins de 7
séances, le tarif A est moins cher, si on va à plus de 7
séances, le tarif B est moins cher.
Retour index chapitres


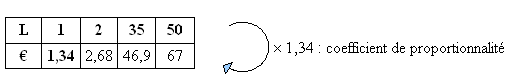
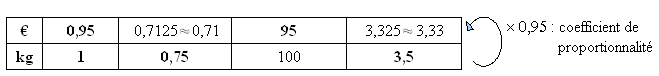

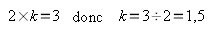


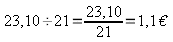
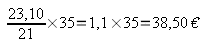


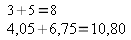 Les kg s'additionnent, donc les € s'additionnent !
Les kg s'additionnent, donc les € s'additionnent !
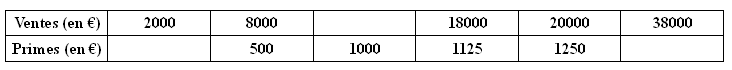


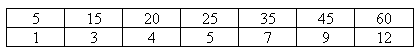
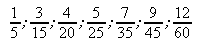 sont égales ou que les fractions
sont égales ou que les fractions 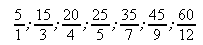 sont égales.
sont égales.
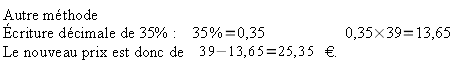
 Le nouveau prix est donc de :
Le nouveau prix est donc de :