Le signe

se lit « est inférieur à ou égal à »
INEGALITES LARGES
Le signe
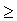
se lit « est supérieur ou égal à »
Résolution d’inéquations
Vocabulaire
|
Le signe < se lit « est strictement inférieur à » |
|
|---|---|
|
|
INEGALITES STRICTES |
|
Le signe > se lit « est strictement supérieur à » |
|
|
Le signe |
|
se lit « est inférieur à ou égal à » |
|
|---|---|---|---|
|
|
INEGALITES LARGES |
||
|
Le signe |
|
se lit « est supérieur ou égal à » |
|
« inférieur » signifie « plus petit que »
« supérieur » signifie « plus grand que »
Opérations sur les inégalités
|
Propriété 1 : |
quels que soient les nombres a, b et c |
||
|
|
|
équivaut à |
|
|
Exemple 1: |
|
|---|
|
Propriété 2 : |
Quels que soient les nombres a et b :
1°- pour tout nombre c strictement positif ( c 0 ) : |
||
|
|
équivaut à |
|
|
|
On NE CHANGE PAS le sens de l’inégalité !
2°- pour tout nombre c strictement négatif ( c 0 ) : |
|||
|
|
équivaut à |
|
|
|
|
|||
|
Exemple 2: |
|
On divise par 3 (ou on multipie par l'inverse de 3), nombre positif : on ne change pas le sens de l'inégalité. |
|
|---|---|---|---|
|
Rappel : l'inverse de 3 est |
|
||
|
Exemple 3: |
|
On divise par -7 (ou on multipie par l'inverse de -7), nombre négatif : on change le sens de l'inégalité. |
|
|---|---|---|---|
|
Rappel : l'inverse de -7 est |
|
||
Résolution
d’inéquations : on utilise les deux règles
énoncées au-dessus.
|
Exemple 4: |
|
|---|
|
Exemple 5: |
|
|---|
Représentation graphique des solutions
On utilise une droite graduée.
Légende : les solutions sont coloriées en rouge.
|
|
Inégalité stricte, le crochet est tourné vers ce qui n'est pas solution ! |
|---|---|
|
|
|
|
|
Inégalité stricte, le crochet est tourné vers ce qui n'est pas solution ! |
|---|---|
|
|
|
|
|
Inégalité large, le crochet est tourné vers ce qui est solution ! |
|---|---|
|
|
|
|
|
Inégalité large, le crochet est tourné vers ce qui est solution ! |
|---|---|
|
|
|