fractions

Fractions

I- Définitions

Définition 1 :

Le quotient du nombre a par le nombre non nul b s’écrit sous forme fractionnaire

Exemple : 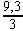est une écriture fractionnaire du quotient de 9,3 par 3 donc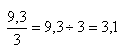

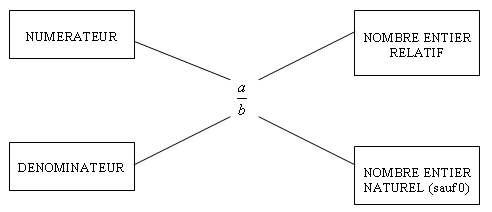
Définition 2 :

Lorsque a est un entier relatif et b un entier naturel non nul , est une fraction.

Exemples :	sont des fractions.
	est une écriture qui existe, mais qui ne s’appelle pas une fraction.

En résumé :

Remarques : a) Les fractions désignent exactement le même nombre. Ce nombre pourrait s’écrire aussi , mais cette dernière notation n’est pas utilisée.

b) Tous les nombres entiers peuvent s’écrire comme fraction. Par exemple, 2 peut s’écrire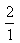

II- Fractions égales

1- Réduction au même dénominateur

Formule :

Autrement dit :

Propriété 1 :

Lorsqu’on multiplie ou divise le numérateur et le dénominateur d’une fraction par un même nombre, on obtient une fraction égale.

Cette formule permet de :

• simplifier une fraction ;

Exemple :

• réduire deux fractions au même dénominateur.

Exemple : Réduire au même dénominateur .

Pour déterminer le plus petit dénominateur commun à 12 et 8, j’écris simultanément les tables de multiplications de 12 et 8 et je m’arrête lorsque j’obtiens le même résultat.

Le plus petit dénominateur commun à ces deux fractions est 24. On en déduit que :

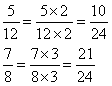
2- Comparaison de deux fractions

• Si elles ont le même dénominateur, la plus petite est celle dont le numérateur a la plus petite valeur absolue.

Exemples :	a)
	b)

• Si elles n’ont pas le même dénominateur, on peut comparer le quotient ou les réduire au même dénominateur.

Exemples :

a) Comparons

b) Comparons et

donc

III- Addition et soustraction de fractions

Règle :	On ne sait additionner ou soustraire deux fractions que si elles ont le même dénominateur
Règle :	Pour *additionner* ( ou soustraire ) *deux fractions* ayant le *même dénominateur, on additionne* ( ou soustrait ) les *numérateurs* et on *garde le dénominateur commun.*

Propriété 2 :

Exemples :	a)
	b)

Si les fractions n’ont pas le même dénominateur, il faut commencer par les réduire au même dénominateur !

Exemples :	a)
	b)
	c)
	d)

IV- Multiplication de fractions

Règle :

Pour multiplier deux fractions entre elles, on multiplie les numérateurs entre eux et les dénominateurs entre eux.

Propriété 3 :

Exemple :

Cas particulier : fraction d’une quantité

Règle :

Pour calculer une fraction d’une quantité, il faut multiplier cette quantité par la fraction.

Exemples :

b) Une barrique a une contenance de 225 L.

Combien de litres contiennent les de la barrique ?

Les de la barrique représentent 135 litres.

c) 30 % des concurrents d’une course cycliste étaient des Espagnols. Les deux tiers d’entre eux ont terminé l’épreuve. Quelle fraction de tous les partants correspond aux coureurs Espagnols ayant terminé la course ?