Exemple d'équation :
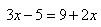
Equations du premier degré à une inconnue
I- Généralités
|
Exemple d'équation : |
|
|---|
Résoudre une équation, c’est trouver la ( ou les ) valeur(s) de l’inconnue qui vérifie(nt) l’égalité donnée.
Ces valeurs sont les solutions de l'équation.
|
Définition : |
|
On
appelle équation du premier degré à une
inconnue x toute égalité de la forme : avec
a et b nombres quelconques,
|
Si on cherche les solutions d’une équation du 1er degré à une inconnue dans l’ensemble de tous les nombres (c’est-à-dire l’ensemble noté IR), alors cette équation admet toujours une et une seule solution.
II- Opérations sur les égalités
1- Addition-soustraction d’un même nombre
|
Propriété 1 : |
Si On peut ajouter aux deux membres d’une égalité un même nombre |
|
Exemple : |
|
|
|
Si On peut soustraire aux deux membres d’une égalité un même nombre |
|
Exemple : |
|
|
Conséquence : |
Pour résoudre une équation, on peut regrouper d’un côté tous les termes où figure l’inconnue et de l’autre côté tous les autres termes. |
|
Exemple :
|
|
1°- On ajoute -2x à chaque membre 2°- On réduit et tous les termes en x sont à gauche 3°- On ajoute 5 à chaque membre 4°- On réduit et tous les termes sans x sont à gauche |
Vérification :
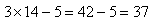 et
et 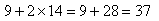
2- Multiplication-division par un même nombre
|
Propriété 2 : |
Si
On peut multiplier les deux membres d’une égalité par un même nombre. |
|
Exemple : |
On supprime le dénominateur commun en multipliant les deux membres par 5. |
|
|
Si On peut diviser les deux membres d’une égalité par un même nombre non nul. |
|
Exemple : |
On trouve x en divisant les deux membres de l’égalité par 5. |
|
Propriété 3 :
|
Si |
Si les deux quotients sont égaux, alors les produits en croix sont égaux.
Exemple :
|
|
|
|
|
Vérification :
|
III- Equation produit
|
Propriété 4 : |
Un produit de plusieurs facteurs est nul si et seulement si l’un des facteurs est nul. |
Exemple :
|
|
|
Exemple
1 : résoudre dans IR l’équation 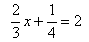
|
• On réduit tous les nombres (coefficients) au même dénominateur. • On "simplifie" par le dénominateur commun. |
L’équation
|
Exemple
2 : résoudre dans IR l’équation 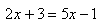
|
• On se débrouille pour transposer "tous les x " à gauche du symbole de l’égalité. |
|
Il faut ensuite traduire l’énoncé à l’aide d’une équation à résoudre.
Exemple 3 : Un grand-père et son petit-fils ont 56 ans à eux deux. Le petit-fils a 50 ans de moins que son grand-père. Quel est l’âge du grand-père ?
Notons x l’âge du petit-fils.

Le petit-fils a 3 ans et le grand-père 53 ans
• Attention : dans certains énoncés, des contraintes peuvent être imposées concernant la nature du résultat à trouver.
Exemple 4 : peut-on trouver un entier naturel tel que la somme de cet entier avec les deux entiers consécutifs soit égale à 13 ?
Notons x cet entier naturel.

Or 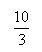 n’est pas un entier !
n’est pas un entier !
Ce problème n’admet pas de solution !
Retour index chapitres