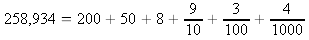
Nombres entiers et décimaux
1- Ecriture décimale
Tout nombre décimal peut s'écrire en deux parties séparées par une virgule.
Les chiffres situés à gauche de la virgule constituent la partie entière du nombre, ceux situés à droite de la virgule constituent la partie décimale du nombre.
Exemples : 625,813 14,003
partie entière 625 partie décimale 813 partie entière 14 partie décimale 003
Selon sa position dans la partie entière, un chiffre indique :
les unités, les dizaines, les centaines,...
Selon sa position dans la partie décimale, un chiffre indique :
les dixièmes, les centièmes, les millièmes,...
Exemple : 258,934 signifie 2 centaines, 5 dizaines, 8 unités, 9 dixièmes, 3 centièmes, 4 millièmes
Exercice 1
2,456 signifie répondre
Exercice 2
35,06 signifie répondre
L'écriture 258,934 peut aussi se traduire par l'égalité suivante :
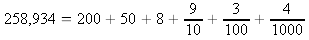
A partir de l'exemple précédent, décomposer les nombres suivants :
Exercice 3
2,456 = réponse
Exercice 4
35,06 = réponse
Exercice 5
2543,107 = réponse
Attention : un nombre entier est
un nombre décimal
!
En effet, un nombre entier est un nombre décimal dont la partie décimale est nulle.
Par exemple : 53 = 53,0
2- Ecriture fractionnaire
Une fraction décimale est une fraction dont le dénominateur est 10, 100, 1 000,... et dont le numérateur est un nombre entier.
Exemple : 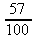
Tout nombre décimal peut s'écrire sous la forme d'une fraction décimale.
Exemple : 
Exercices
Ecrire sous forme de fraction décimale les nombres suivants :
45,17 = réponse
6,387 = réponse
12,7 = réponse
Les nombres décimaux sont les seuls nombres qui peuvent s'écrire sous la forme d'une fraction décimale.
Attention : un nombre décimal n'est pas forcément un nombre à virgule !
Exemple : 34 est un nombre décimal
un nombre à virgule n'est pas forcément un nombre décimal !
Exemple : est un nombre à virgule, mais ce n'est pas un nombre décimal : il ne peut pas s'écrire sous la forme d'une fraction décimale.
3- Multiplication et division par 10 ; 100 ; 1 000 ; 0,1 ; 0,01 ; 0,001
a) Multiplication par 10 ; 100 ; 1 000
Pour multiplier un nombre par 10 ; 100 ou 1 000, il faut déplacer la virgule de ce nombre respectivement de 1, 2 ou 3 rangs vers la droite.
Exemples : 5,43 × 10 = 54,3 35 × 100 = 3 500 12,0365 × 1 000 = 12 036,5
Exercices
Calculer : 12,3 × 100 = répondre 0,345 × 10 = répondre 34,0123 × 1 000 = répondre
0,004 × 100 = répondre 4,56 × 1 000 = répondre 5,2 × 100 = répondre
0,0023 × 1 000 = répondre 5,67 × 10 = répondre 234 × 1 000 = répondre
Attention : diviser par 0,1 ; 0,01 ou 0,001 revient à multiplier respectivement par 10 ; 100 ou 1 000.
Exemples : 5,43 : 0,1 = 5,43 × 10 = 54,3 35 : 0,01 = 35 × 100 = 3 500
Exercices
Calculer : 27,54 : 0,01 = répondre 3,9 : 0,001 = répondre
0,78 : 0,1 = répondre 456,78 : 0,01 = répondre
Pour diviser par 10 ; 100 ou 1 000, il faut déplacer la virgule respectivement de 1, 2 ou 3 rangs vers la gauche.
Exemples : 456,89 : 100 = 4,5689 23 : 1 000 = 0,023 3,67 : 10 = 0,367
Exercices
Calculer : 8,34 : 1 000 = répondre 13,5 : 10 = répondre 1,2 : 100 = répondre
12,89 : 10 = répondre 54,3 : 1 000 = répondre 3,5 : 100 = répondre
Attention : multiplier par 0,1 ; 0,01 ou 0,001 revient à diviser respectivement par 10 ; 100 ou 1 000.
Exemples : 35 × 0,1 = 35 : 10 = 3,5 631,5 × 0,001 = 631,5 : 1 000 = 0,6315
Exercices
Calculer : 567,4 × 0,01 = répondre 54,08 × 0,1 = répondre
98,34 × 0,001 = répondre 0,3 × 0,01 = répondre
Ordre des nombres décimaux
4- Droite graduée
Sur une droite graduée, chaque point est repéré par un nombre que l'on appelle abscisse.
Exemples :
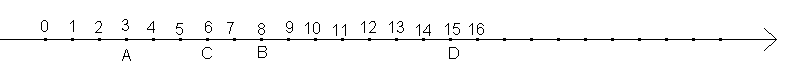
L'abscisse du point A est 3. L'abscisse de B est 8. L'abscisse du point C est 6. L'abscisse de D est 15.
5- Comparaison de nombres décimaux
Pour comparer deux nombres décimaux, on commence par comparer leur partie entière.
a) Dans le cas où les parties entières sont différentes, le plus grand des nombres est celui qui a la plus grande partie entière.
Exemple : Comparons 31,315 et 43,7.
La partie entière de 31,315 est 31
La partie entière de 43,7 est 43
31 est plus petit que 43 donc 31,315 est plus petit que 43,7
On écrit : 31,315 < 43,7
b) Dans le cas où les parties entières sont égales, on compare les parties décimales.
On complète les parties décimales avec des 0 pour qu'elles aient le même nombre de chiffres.
Le plus grand des nombres est celui qui a la plus grande partie décimale.
Exemple : Comparons 27,3 et 27,219.
La partie entière de 27,3 est 27
La partie entière de 27,219 est 27
Les deux nombres ont donc la même partie entière.
On doit donc comparer leur partie décimale
On a : 27,3 =27,300
300 est plus grand que 219 donc 27,3 est plus grand que 27,219
On écrit : 27,3 > 27,219
Autre méthode : on compare les parties décimales chiffre après chiffre en commençant par les dixièmes, puis les centièmes,... (de la gauche vers la droite).
Le symbole < signifie : « est inférieur à » ou « est plus petit que »
Le symbole > signifie : « est supérieur à » ou « est plus grand que »
Exemples : 3,99 < 7,54 car 3 < 7
34,65 < 34,71 car 6 dixièmes est plus petit que 7 dixièmes
6- Classement des nombres décimaux
a) Par ordre décroissant
Pour classer des nombres par ordre décroissant, on les range du plus grand au plus petit.
Exemple : 3,6 > 3,598 > 2,99
b) Par ordre croissant
Pour classer des nombres par ordre croissant, on les range du plus petit au plus grand.
Exemple : 25,84 < 25,9 < 42,01
7- Encadrement, troncature, arrondi
a) Encadrement
Trouver un encadrement d'un nombre, c'est donner un nombre plus petit et un nombre plus grand que celui-ci.
Exemples : 10 < 14,56 < 20 Encadrement à la dizaine
14,5 < 14,568 < 14,6 Encadrement au dixième
14,56 < 14,561 < 14,57 Encadrement au centième
b) Troncature
La troncature à l'unité d'un nombre est sa partie entière.
Exemple : la troncature à l'unité de 58,945 est 58.
c) Arrondi
L'arrondi à l'unité d'un nombre est :
le nombre entier le précédant si le chiffre des dixièmes est 0, 1, 2, 3 ou 4 ;
le nombre entier suivant si le chiffre des dixièmes est 5, 6, 7, 8 ou 9.
Exemples
: a) l'arrondi
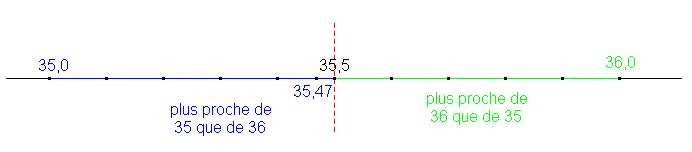
à l'unité de 35,47 est 35
Explications : encadrement à l'unité : 35 < 35,47 < 36 (35 est la troncature à l'unité du nombre)
L'arrondi à l'unité de 35,47 est 35,0 car le 1er chiffre après la virgule est un 4.
| Nombres | Arrondis à l'unité |
| 35,071 | 35 |
| 35,399 | 35 |
| 35,471 | 35 |
| 35,5 | 36 |
| 35,691 | 36 |
| 35,807 | 36 |